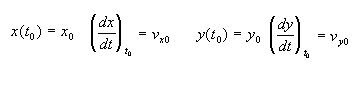Introducción

Los métodos numéricos constituyen una herramienta muy valiosa para la resolución de problemas prácticos de Ingeniería, se pueden definir a los métodos numéricos como las técnicas mediante las cuales es posible formular problemas de manera que puedan resolverse utilizando operaciones aritméticas, ó también como el grupo de conocimientos matemáticos relacionados con el diseño y análisis de algoritmos necesarios para resolver problemas de ciencia e ingeniería por ello el objetivo de este Blog es el de presentar de manera sencilla el método numérico de Runge-Kutta y la implementación de los sistemas numéricos en el computador

Las Ecuaciones Diferenciales

Ecuaciones diferenciales

Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones. Dependiendo del número de variables independientes respecto de las que se deriva.

Las ecuaciones diferenciales se dividen en:

Ecuaciones Diferenciales Ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.

Ecuaciones en Derivadas Parciales: aquellas que contienen derivadas respecto a dos o más variables.

Orden

El orden de una ecuación diferencial es el de la derivada más alta  contenida en ella.

Grado

El grado de una ecuación diferencial es una potencia a la que esta elevada la derivada más alta, siempre y cuando la derivada este dada en forma polinomial.

Hay otra clasificación importante de las ecuaciones diferenciales ordinarias la cual se basa en si éstas son lineales o no lineales. Se dice que la ecuación diferencial.

Es lineal cuando F es una función lineal en las variables y,y´,y(n). Por lo tanto, la ecuación diferencial ordinaria lineal de orden n es 3.La ecuación que no es de la forma (3), es una ecuación no lineal.

         Un problema físico sencillo que de origen a una ecuación diferencial no lineal es el péndulo oscilante.

Ecuación Diferencial Lineal

La forma general de una ecuación diferencial lineal de orden n es como sigue:

 

Recuérdese que linealidad quiere decir que todos los coeficientes solo son funciones de x, y que y todas sus derivadas están elevadas a la primera potencia. Entonces, cuando n = 1, la ecuación es lineal y de primer orden.

 

Sobre las Ecuaciones Diferenciales

Ecuaciones diferenciales

Solución:

Se define como una relación sin derivadas entre las variables que satisface a la ecuación

Solución Particular:

Se obtiene de la primitiva dando valores definidos a las constantes arbitrarias (Ecuación de una curva llamadas curvas integrales de la ecuación diferencial)

Solución General:

 Solución que contiene todas o casi todas sus soluciones (primitiva).

Interpretación Geométrica:

Las ecuaciones diferenciales se expresan geométricamente mediante la interpretación de un problema mediante trazos en una recta. Así a cada punto del plano le corresponde una pendiente. 

Trayectorias:

Cualquier curva que corte a cada uno de los miembros de una familia dada de curvas bajo un ángulo constante w, se llama una trayectoria w de la familia.

La trayectoria de intersección, que forma un ángulo de 90º de una familia y sus pendientes son perpendiculares entre si se denomina “Trayectoria Ortogonal”. 

Para hallar las trayectorias ortogonales se utilizara las curvas integrales de la ecuación diferencial:

f(x,y, y´-tgw/1+y`tgw)=0

Existencia:

Se dice que hay existencia cuando existe una solución real para la expresión y se cumplen las siguientes condiciones:

Continuidad de f(x,y) en R

Acotamiento de f(x,y) por R

Unicidad:

Se dice que existe unicidad, cuando se cumple lo siguiente:

Continuidad de f(x,y) y ȭf/ ȭy en R

 Acotamiento de f(x,y) y ȭf/ ȭy por R

Aunque existen excepciones donde solo se cumple una de las condiciones o ninguna de las dos.

Campo Direccional:

 Al conjunto de los segmentos que resultan de la terna (x,y,y´)

Método de Runge Kutta

   

           Métodos de Runge-Kutta

Los Runge-Kutta no es sólo un método sino una importante familia de métodos iterativos tanto implícitos como explícitos para aproximar las soluciones de ecuaciones diferenciales ordinarias (E.D.O´s), estas técnicas fueron desarrolladas alrededor de 1900 por los matemáticos alemanes Carl David Tolmé Runge y Martin Wilhelm Kutta

El objetivo de los métodos numéricos de runge-kutta, es el análisis y solución de los problemas de valor inicial de ecuaciones diferenciales ordinarias (EDO), estos son una extensión del método de euler para resolver las (EDO’S), pero con un orden de exactitud más alto que este.

La convergencia lenta del método de Euler y lo restringido de su región de estabilidad absoluta nos lleva a considerar métodos de orden de convergencia mayor. El método de Euler se mueve a lo largo de la tangente de una cierta curva que esta "cerca" a la curva desconocida o buscada. Los métodos Runge-Kutta extienden esta idea geométrica al utilizar varias derivadas o tangentes intermedias, en lugar de solo una, para aproximar la función desconocida. Los métodos Runge-Kutta más simples se obtienen usando dos de estas derivadas intermedias.

Los  métodos de Runge-Kutta mejoran la aproximación del método de Euler para resolver de modo aproximado el P.V.I.  y' = f(t, y),   y(t0) = y0,  sin necesidad de calcular derivadas de orden superior.

Recordemos que, de acuerdo con la teoría, la expresión general de los métodos explícitos de las etapas de Runge Kutta es:

 

       FUNDAMENTO

Al resolver un PVI o un PF, el objetivo es hallar una función y(t) que verifique en [a,b] los requisitos del  problema. Conscientes de la imposibilidad de obtener una fórmula que exprese y(t), nos contentaremos con obtener los valores que la solución toma en algunos puntos de [a,b]; es decir, obtendremos una tabla de valores de y(t) en [a,b]. Esto puede parecer, a primera vista, frustrante, pero para la mayor parte de las necesidades reales es completamente suficiente; pensemos que realmente, incluso para una función expresada mediante una fórmula, un ordenador solo puede dar sus valores en un número finito de puntos, ya que maneja un número limitado de cifras. El valor de la solución en un punto c distinto de los considerados se obtiene mediante interpolación, o resolviendo de nuevo el problema en el intervalo [a,c].

Así, una técnica de solución consiste en dividir el intervalo [a,b] mediante una malla de puntos a = t0 < tl < … < tn = b, llamados puntos soporte, y obtener los valores yi = y(ti), i = 1, 2, …, n, de la solución en los puntos de la malla.

Una manera frecuente y sencilla (no la mejor en todos los casos) de tomar los ti, consiste en dividir el intervalo [a,b] en n partes iguales, siendo n un natural. Así, los puntos son ti = a + ih, i = 0, …, n. Al valor h =(b - a)/n se lo denomina paso de integración. Utilizaremos en lo sucesivo paso constante en todos los casos.

 

 Los métodos de Runge-Kutta logran la exactitud del procedimiento de una serie de Taylor sin requerir el cálculo de derivadas superiores. Existen muchas variaciones, pero todas se pueden denotar en la forma generalizada de la ecuación:

y_{i + 1} = y_i + φ(x_i,y_i,h)h

Donde φ(xi,yi,h) es conocida como función incremento, la cual puede interpretarse como una pendiente representativa sobre el intervalo.

Donde las a son constantes y las k son:

k₁ = f(x_i,y_i)

k₂ = f(x_i + p₁h,y_i + q₁₁k₁h)

k₃ = f(x_i + p₂h,y_i + q₂₁k₁h + q₂₂k₂h)

Observe que las k son relaciones de recurrencia, esto es, k₁ aparece en la ecuación para k₂, la cual aparece en la ecuación para k₃, etc.

Como cada k es una evaluación funcional, esta recurrencia hace que los métodos Runge-Kutta sean eficientes para la programación. Existen varios tipos de métodos Runge-Kutta al emplear diferentes números de términos en la función incremento como la especificada por n.

n = 1, es el método de Euler. Una vez se elige n, se evalúan las a, p y q al igualar la función incremento a los términos en la serie de Taylor

     Condiciones de orden

Los métodos de Runge-Kutta son métodos de un paso con función de incremento

Si hacemos hn = 0, entonces ki = f(xn,yn) para todo   i = 1,2,...,s. Así,

Por tanto, un método de Runge-Kutta es consistente si y solo si

Por otra parte, puesto que las etapas ki son evaluaciones de la función f, no es difícil convencerse de que φ satisface una condición de Lipschitz con respecto a su segunda variable si f satisface una condición de Lipschitz en y. Así pues, la condición de consistencia es suficiente para garantizar la convergencia. Veamos que también es necesaria.

Métodos de Runge-Kutta de 2do. Orden

          Métodos de Runge-Kutta de 2do. Orden

El método de Runge Kutta es un método numérico de resolución de ecuaciones diferenciales que surge como una mejora del método de Euler. El método de Euler se puede considerar como un método de Runge Kutta de primer orden, el de Heun, es un método de Runge Kutta de orden dos.

La expansión en serie de Taylor de una función y(x) alrededor de un punto x=x₀ , truncada en el tercer término, es decir, en la segunda derivada

Esquema de Discretización del Método de Runge-Kutta de orden 2:

 

y_i  es la coordenada “y” del punto anterior

xi  es la coordenada “x” del punto anterior

 F(x_i,y_i)  es la derivada evaluada en el punto anterior

 F(xi+h/2,yi+k₁/2)  es la derivada evaluada en el punto anterior con el cambio de variable

Ecuación diferencial de segundo orden

Vamos a aplicar el procedimiento de Runge-Kutta a una ecuación diferencial de segundo orden.

Una ecuación diferencial de segundo orden es equivalente a un sistema de dos ecuaciones diferenciales de primer orden, por lo que aplicaremos el mismo esquema.

 

Comparando esta tabla con la de un sistema de dos ecuaciones diferenciales de primer orden, vemos que la segunda columna es la misma, excepto por cambio de nombre de la función, f en vez de g, y de la variable, v en vez de y. En la primera columna, las variables k₁, k₂, k₃, k₄ pueden calcularse directamente sin efectuar llamadas a una función.

  

Sistema de dos ecuaciones diferenciales de segundo orden

Sea el sistema de dos ecuaciones diferenciales de segundo orden

 Con las condiciones iniciales

Este sistema, se puede transformar en un sistema equivalente formado por cuatro ecuaciones diferenciales de primer orden. Aplicando dos veces el esquema descrito para una ecuación diferencial de segundo orden, obtenemos el esquema descrito en las siguientes tablas

 

Conclusión

Finalmente y para concluir se determino que, la resolución de problemas de ingeniería está asociada, por lo general, a resultados numéricos puesto que se requieren respuestas prácticas.

La mayor parte de las leyes científicas de expresan en términos de rapidez de variación de una variable con respecto otra.

Además proporcionan una herramienta esencial para modelar muchos problemas en Ingeniería, Física, Economía y Biología, puesto que estos, por lo general, requieren la determinación de una función que satisface a una ecuación diferencial.

El Método de Runge Kutta es mejor que el método de Euler, pero aún así es posible aumentar la precisión achicando los pasos entre los puntos o implementando el método de orden superior.

Es el método más utilizado para resolver numéricamente problemas de ecuaciones diferenciales ordinarias con condiciones iniciales es el método de Runge-Kutte, el cual proporciona un pequeño margen de error con respecto a la solución real del problema y es fácilmente programable en un software para realizar iteraciones necesarias.

El dominio de los métodos numéricos, en combinación con las capacidades y potencialidades de la programación de computadoras resuelve problemas de ingeniería de manera más fácil y eficientemente.